При классификации волновых моделей, описывающих действующие фазы ценового движения особых проблем не возникало: существовали разночтения в терминологии, неточности в описаниях свойств, расплывчатые формулировки – но все это легко исправлялось. При классификации моделей, описывающих противодействующие фазы ценового движения получилось сложнее: сколько авторов столько и классификаций моделей.
Сначала нужно разобраться, модели каких авторов нужно и можно учитывать. Кого из авторов считать классиками?
Что такое волновой анализ в представлении большинства трейдеров? Ответ очевиден: волновая теория Р. Эллиотта. Однако это представление ошибочно.
Во-первых Р. Эллиотта никак нельзя назвать первооткрывателем. Идею он заимствовал у Д. Доу.
Во-вторых Р. Эллиотт, сделав ряд очень важных наблюдений, лишь описал их, ни дав объяснений, ни составив чёткой классификации волновых моделей, ни полного свода правил их распознавания.
Его последователи, которых рассматривают как «классиков EWA: А. Фрост и Р. Пректер, Р. Балан и другие, лишь дорабатывали и дополняли его наблюдения. В
результате получилось уже не совсем то, что предлагал Р. Эллиотт, но также не подкрепленное обоснованиями. Изменения, привнесённые ими, почему-то не
отделяют от наблюдений Р. Эллиотта.
Были и другие разработчики волновой теории, которые в преобразовании наблюдений Р. Эллиотта пошли другими путями: Том Джозеф, Роберт Майнер, Мирча
Долока. И, конечно Гленн Нили. Причём этих авторов, пытавшихся обосновать теорию, почему-то к «классикам» не относят, но полагают, что всё описанное в
литературе полностью относится к теории разработанной Р. Эллиоттом.
Приведу несколько примеров.
Р. Эллиотт рассматривал диагональный треугольник, имеющий структуру :3:3:3:3:3 = :5 и перекрытие уровня вершины волны-1 волной-4, как завершающую модель движущей или корректирующей фазы ценового движения. Соответственно как волну-(5) или волну-(С). Логика проста, диагональный треугольник, как волновая модель, описывает состояние неуверенности в продолжении данного направления ценового движения.
А. Фрост и Р. Пректер предложили новую модель: диагональный треугольник со структурой :5:3:5:3:5 = :5, перекрытием уровня вершины волны-1 волной-4 и
местоположением как волны-(1) или волны-(А). Так появился начальный диагональный треугольник как модель демонстрирующая неуверенность в развороте
ценового движения. Отличие в теории первое.
Р. Балан в книге «Волновой принцип Эллиотта» посвятил целую главу описанию отклонений от правил.
Например, об изменении структуры: волна-(С) в зигзаге может быть двойным или тройным зигзагом. В сложной коррекции (двойном или тройном зигзаге) после первой Х-волны может появиться горизонтальный треугольник как волна-(Y), а в волновой плоскости вместо волны-(B) – диагональный треугольник, ещё и со структурой :5:3:5:3:5 = :5 (приводя при этом подтверждающий рисунок). Почему так? Р. Балан не объясняет, но пишет, что правила подмены структур должны упростить жизнь аналитика. Трактовка обоснования изменений правил более чем оригинальная.
Далее, А. Фрост и Р. Пректер, чтобы облегчить разметку, предложили в двойном и тройном зигзаге, или двойной и тройной тройке заменить маркировку A-B-C-X-A-B-C-X-A-B-C маркировкой W-X-Y-X-Z. При этом волны W, Y, Z – это простые коррекции. Предельно ясно, сложная коррекция состоит из простых. Затем Д.
Возный, в «Коде Эллиотта» пишет, что каждая из волн W-Y-Z может быть сложной коррекцией, например, волна-(W) старшего волнового уровня становиться по
структуре сложной коррекцией, вида w-y-z-x-w-y-z-x-wy-z. Возможно такие сложные коррекции встречаются, но это уже совершенно иные модели.
Это самые безобидные отличия от первоначальной теории Р. Эллиотта. Есть отличия более серьёзные.
Сейчас просто хочется подчеркнуть, что далеко не все трактовки в волновом анализе принадлежат Р. Эллиотту. Многие исследователи дополняли и изменяли его
теорию наблюдений.
В этом плане «усовершенствования» волновой теории Гленном Нили выглядят наименее «безобидными» и наиболее оправданным в сравнении с интерпретациями «классиков». Гленн Нили по концепции гораздо ближе к теории Р. Эллиотта, чем другие «гуру». Однако бытует мнение, что анализ волн Эллиотта по Гленну Нили, это какой-то другой волновой анализ.
Вопреки сложившимся убеждениям, метод Гленна Нили не противоречит традиционному волновому анализу, такое суждение не соответствует действительности. Г. Нили не подвергал сомнению никакие базовые принципы наблюдений Р. Эллиотта, он лишь существенно их дополнил.
Дело в том, что в трудах Р. Эллиотта и его последователей описывается лишь качественная сторона вопроса.
Классический волновой анализ допускает много вольностей при идентификации волновых моделей. Как результат – множество допустимых вариантов разметки и нет достаточных оснований для выбора единого сценария. Гленн Нили, в книге «Мастерство анализа волн Эллиотта» напротив, описал алгоритмический подход
к волновой теории, предполагающий количественное описание известных волновых моделей.
Мнение о «другом методе» обусловлено достаточно сложным изложением материала, введением новых моделей и изменённой терминологией. Например, переименование конечного диагонального треугольника в терминальный импульс. Это переименование логично, но введение таких терминов как: сужающийся треугольник с обратным реверсом, даже комментировать не буду. Конечно можно записать правильно: «треугольник со сходящимися образующими и обратным чередованием волн-(B) и -(D)».
Если в «Мастерстве анализа волн Эллиотта», несмотря на терминологию, разобраться в моделях несложно, то нововведения, последовавшие в NEoWave порой
ставят в тупик новой классификацией и может быть несколько надуманным введением таких моделей как neutral triangle, reverse alternation triangle и т.п.. Так же
спорно введение новых моделей сложной коррекции: Diametric formation как семи волновой модели сложной коррекции, и Symmetrical formation как девяти
волновой модели. Сравнение теорий Г. Нили и Р. Эллиотта можно проводить только по сопоставлению волновых моделей и их свойств, не касаясь других аспектов теории Г. Нили.
Теперь перейдём непосредственно к простым моделям коррекции – моделям, описывающим фазы противодействующего ценового движения.
Казалось бы можно пойти простым путём – у всех авторов взять все модели и свести воедино. Попробовали и при небольших корректировках, с точки зрения
упорядочения классификации, этот способ сработал.
Общая классификация составленная по внутренней структуре моделей:
Простые корректирующие модели:
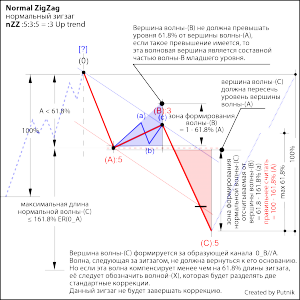
• ZigZag, модель коррекции со структурой :5:3:5 = :3;
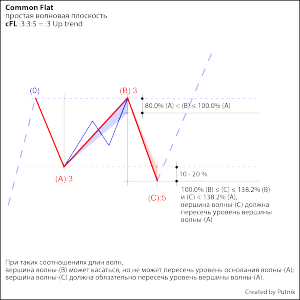
• Flat, модель коррекции со структурой :3:3:5 = :3;
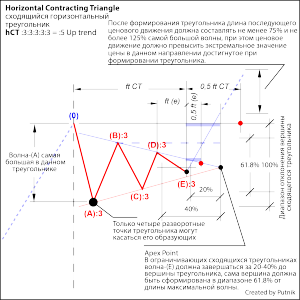
• Horizontal Tringles, модель коррекции со структурой :3:3:3:3:3 = :5.
Сложные корректирующие модели:
• Dodle & Triple ZigZag, как сложные модели глубокой коррекции;
• Dodle & Triple Tree, как сложные модели протяженной коррекции.
С точки зрения терминологии и описания свойств моделей лишь выявилось ещё большее количество проблем. Поэтому решили составить собственную систему классификации простых корректирующих моделей.
Принципы классификации в группах моделей:
- Волна-(А) является первой из формируемых волн модели коррекции. Пока мы не знаем её длину, длительность и структуру. Мы вообще ничего не знаем о том какая будет формироваться модель коррекции, и предположить не можем. Поэтому вся последующая терминология и описание свойств моделей коррекции отталкивается от структуры и длины волны-(А).
- Если волна-(В) не превосходит длину волны-(А) и формируется по правилам классического волнового анализа – эта модель определяется как «правильная».
- Если волна-(В) пересекает основание волны-(А), то формируется «неправильная» модель коррекции и в её название добавляется слово Irregular.
При этом длина волны-(В) не может быть бесконечной и для разных классов моделей коррекции ограничивается по пропорциям относительно длины волны-(А) вполне определёнными значениями. - Если волна-(В), пересекая основание волны-(А) нарушает и эти пропорции, значит формируется подвижная волновая модель и в её название добавляется слово Running – «очень неправильная» модель коррекции. При этом, пропорции длин волны-(В) и волны-(А) также ограничены определёнными значениями для каждого класса моделей коррекции.
- После того как сформированы волны-(А) и –(В), мы знаем их длины, длительности, соотношения длин, взаимное положение волновых вершин и структуру, можно оценить формирование волны-(С).
- Первый принцип по которому волна-(С) распознается как модель одного волнового уровня с волнами-(А) и -(В) – это длина волны-(С). Ни в какой из
волновых моделей коррекции она не может быть меньше 38.2% длины волны-(А). - Если длина волна-(С) составляет от 38.2% до 100% длины волны-(А) – она является «слабой», и в наименовании модели добавится запись (C)-wave Failure.
- Если длина волна-(С) составляет от 100% до 161.8% длины волны-(С) – она является «нормальной», и в наименовании модели дополнительных записей не
производится. - Если длина волна-(С) составляет от 161.8% до 261.8% длины волны-(А) – она является «сильной» — удлинённой, и в наименовании модели добавляется запись (C)-wave Extended.
- В некоторых случаях при формировании волновых плоскостей и волна-(В) может оказаться слабой, в этом случае модель получает расширение в названии как (В)-wave Failure. Если слабыми являются и волна-(В) и волна-(С) – добавляется запись Double Failure.
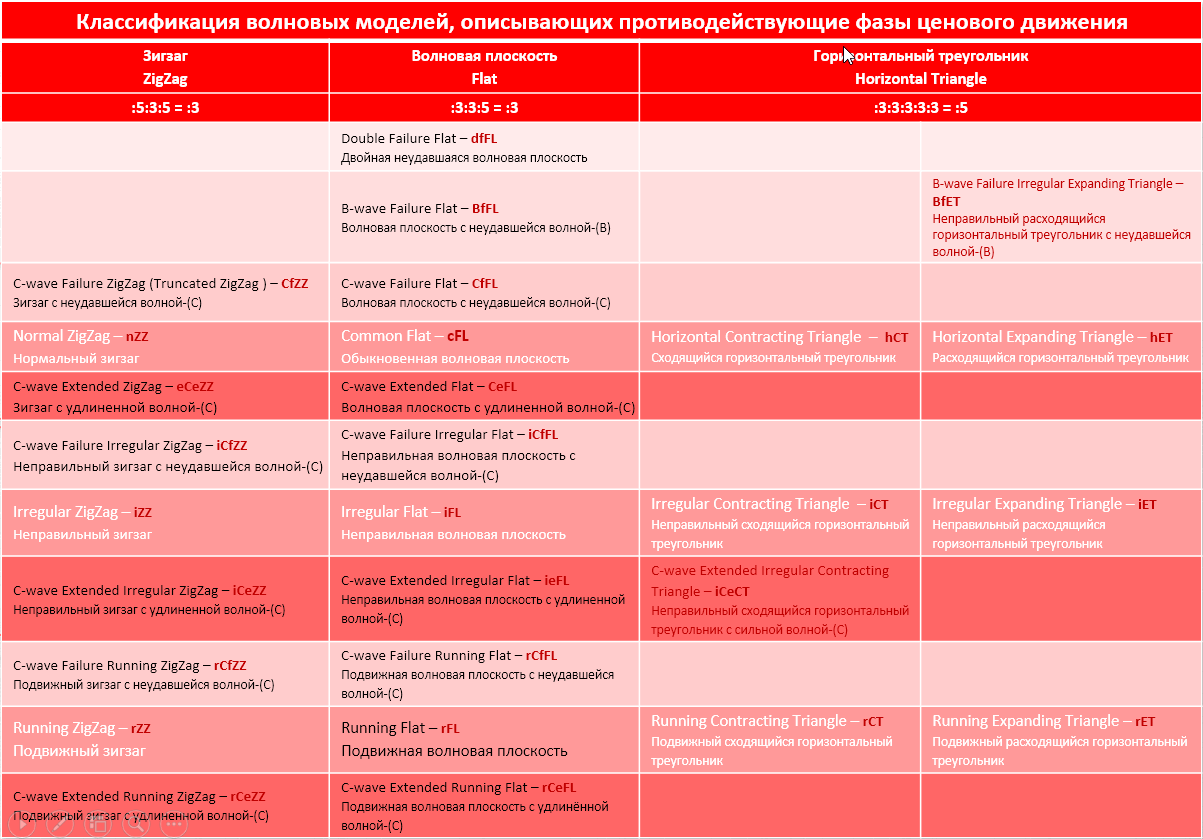
Ниже представлены таблица «Общей классификации корректирующих моделей ценового движения» и таблица «Классификации простых моделей коррекции». Каждый класс в отдельности и сложные модели коррекции будут разбираться в последующих статьях.
 |
 |
 |
Из наименований моделей, приведённых в таблице, становится понятно, что мы отказались от введения «персональных» названий моделей коррекции. Принадлежность корректирующей модели к тому или иному классу определяется по внутренней структуре составляющих волн. Внутри класса разделение моделей идёт в соответствии с соотношением длин составляющих волн и взаимным расположением их волновых вершин. В эту схему прекрасно «укладываются» и зигзаги и волновые плоскости, и горизонтальные треугольники. Все пропорции длин волн заданы с допуском, что исключает и появление «белых пятен», когда невозможно выявить ни одну модель, и неопределенность в распознавании модели, когда можно выбрать и ту, и другую.
В таблице остались пустые ячейки. Заполнять их или нет?
Изначально на реальных графиках не было выявлено моделей «достойных» заполнить пустые ячейки. Хотя, следуя представленной логике рассуждений они должны были выявиться. Это как в таблице элементов Д. И. Менделеева: таблица есть, пустые ячейки есть, но они постепенно заполняются. Не все сразу, и представленная работа по классификации проделана не за один год.
Рассмотрим возможность заполнения ячеек.
|
Например, волна-(В) в классической модели зигзаг может составлять 1-61.8% длины волны-(А). Следовательно, взяв диапазон 1-38.2% длины волны-(А)*, можно выделить модель как «зигзаг со слабой волной-(В) !!! Но нужно ли это в прагматическом смысле для ведения торговли? Думаю, нет. |
 |
Второй пример. Рассмотрим неправильный горизонтальный треугольник в котором волна-(В) больше волны-(А) и волна-(С) больше волны-(В). Образующие A_C и B_D сходящиеся, но такой модели в классической классификации сходящихся горизонтальных треугольников нет. У Глена Нили в NeoWave подобная модель появилась, но названа она нейтральным треугольником. На графиках такие модели также реально встречаются. Следовательно, такая модель может быть идентифицирована. Ячейку в классификаторе можно заполнить !!! |
Классификация составлена.
О возможности заполнения ячеек, допустимых предельных значениях пропорций волн, конкретных моделях каждого класса мы продолжим разговор в следующих публикациях.
Но начнём с примеров, поясняющих, а для чего всё это нужно:
 |
 |
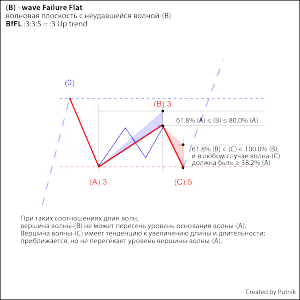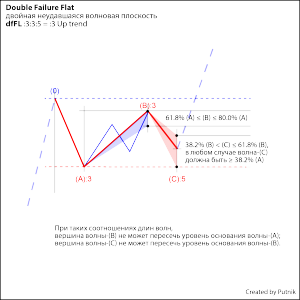
Волновая плоскость, простые модели протяженной коррекции: Double Failure Flat и (B)-wave Failure Flat.
В данном примере представлены модели волновой плоскости со слабыми волнами-(В) и –(С) и слабой волной-(В).
Типичная ошибка при идентификации: считать волну-(В) со структурой :3 первой волной последующего восходящего движения !!!
Она тройка и не перекрывает предшествующего экстремума !!! Следовательно, коррекция ещё не завершена – нет подтверждения её завершения по правилу взаимного положения волновых вершин одного волнового уровня.
Основная проблема этой ошибки не просто в неправильном распознавании модели. Неправильное распознавание — это неправильная установка инструментов прогнозирования (не к тем вершинам), что приводит к неправильным целям.
 |
 |
Но проблема может быть и серьезнее.
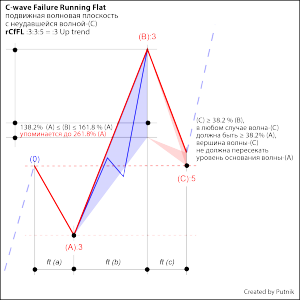
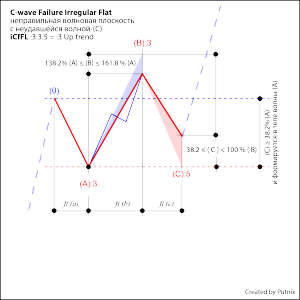
Неправильная волновая плоскость со слабой волной-(С) и подвижная волновая плоскость со слабой волной-(С) — коварные модели для распознавания.
Первая волна коррекции -(А) является тройкой и может быть принята за всю коррекцию если не учитывать её пропорции к предшествующему ценовому движению.
Далее, не обратив внимание на то, что волна-(В), перекрывая основание волны-(А), также является тройкой — принимают конфигурацию как волны-4 и -5, устанавливая цели на разворот. Усугубляет сложность распознавания волна-(С) формируемая в волновой плоскости как пятерка. Ожидание разворота 100%! НО!
Основная проблема этой ошибки не просто в неправильном распознавании разворота — эта модель указывает на слабость коррекции и силу последующего движения, обычно сопровождающегося удлинением волны. Последствия вполне ясны!
Трейдер, вставший на разворот оказывается перед началом мощнейшего продолжения движения.
Игорь Бебешин (Putnik)
E-mail: [email protected]
http://www.dml-ewa.ru/
Skype: fibonacciclub
Оставить комментарий